What is non-Hamiltonian molecular dynamics

Although (Hamiltonian) molecular dynamics has proven to be a very useful tool, it has one basic restriction: It can in principle generate only equilibrium properties of the microcanonical ensemble.

If one wishes to do molecular dynamics simulations on other equilibrium ensembles, subtle techniques are required. Typically these involve extending the phase space beyond the 2dN dimensions of the physical system and writing an extended Lagrangian, from which the equations of motion are derived.

Although the mechanical consequences of this procedure might be straightforward, the implications on the statistical mechanics of the system are less evident. In general the extended Lagrangians cannot be transformed into Hamiltonian form; hence the name non-Hamiltonian molecular dynamics. Consequently, building a connection to statistical mechanics through the classical formalism is not feasible.

Currently the use of non-Hamiltonian dynamical systems to perform molecular dynamics simulations is becoming more or less standard. In addition to constructing desired equilibrium ensembles, non-Hamiltonian methods are also used to describe systems subject to holonomic constraints, driven systems or systems away from equilibrium.

As concrete examples of the usage of non-Hamiltonian methods one can take modeling of sheared systems, such as lubrication studies. Or just as well one might consider the various biologically motivated molecular dynamics simulations, say studies of protein designability and folding.

Animations:

Below are snapshots from a simple non-Hamiltonian simulation, a polymer stretching and collapsing under shear flow in constant temperature.

• video

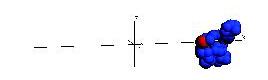
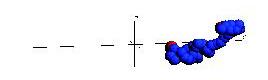
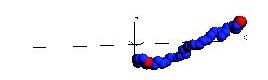
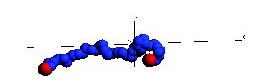
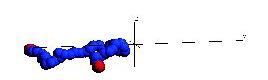
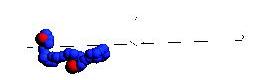
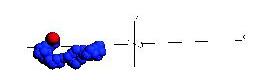
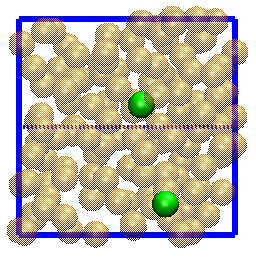
Below is a simulation of a simple molecular system under shear flow (Lees-Edwards boundary conditions). The plane of zero shear is in the middle (dashed line). Click the picture to start the animation. Two particles are marked with green color to illusrate the behavior of the individual particles.

• See our publication list.

General references:

• C. Mundy, S. Balasubramanian, K. Bagchi, M. Tuckerman, G. Martyna and M. Klein, "Non-equilibrium molecular dynamics", Reviews in Computational Chemistry 14 (2000) 291-397
• G. Ciccotti and G. Kalibaeva, "Molecular dynamics of complex systems: Non-Hamiltonian, constrained, quantum-classical". In M. Karttunen, I. Vattulainen and A. Lukkarinen, editors, Novel methods in soft matter simulations , chapter 5, pages 146-185 (2004)